QR分解的三种实现算法
本文主要介绍QR分解的三种实现算法:经典Gram-Schmidt算法、改良版Gram-Schmidt算法和Householder变换算法。全文以4x3矩阵$A$为例。
import numpy as np
A = np.array([[1, 0, 1],
[2, 0, 0],
[0, 1, 0],
[1, -1, 1]], dtype=float)
A # 4 x 3
输出结果:
array([[ 1., 0., 1.],
[ 2., 0., 0.],
[ 0., 1., 0.],
[ 1., -1., 1.]])
经典Gram-Schmidt算法(CGS)
例子
经典Gram-Schmidt算法和Gram-Schmidt正交化相关,基本思想是将还未正交化的向量扣除其在已经正交化的向量上的投影,再对其单位化。以矩阵$A$为例:
第一步:将$v_1$标准化得到$q_1$
v1 = A[:, 0]
q1 = v1 / np.linalg.norm(v1)
print("v1:", v1)
print("q1:", q1)
print("length of q1:", np.linalg.norm(q1))
输出结果:
v1: [1. 2. 0. 1.]
q1: [0.40824829 0.81649658 0. 0.40824829]
length of q1: 1.0
第二步:将$v_2$扣除其在$q_1$上的投影,再单位化得到$q_2$
v2 = A[:, 1]
q2 = (v2 - (q1.T @ v2) * q1) / np.linalg.norm(v2 - (q1.T @ v2) * q1)
print("v2:", v2)
print("q2:", q2)
print("length of q2:", np.linalg.norm(q2))
输出结果:
v2: [ 0. 0. 1. -1.]
q2: [ 0.12309149 0.24618298 0.73854895 -0.61545745]
length of q2: 0.9999999999999999
第三步:将$v_3$扣除其在$q_1$、$q_2$上的投影,再单位化得到$q_3$
v3 = A[:, 2]
q3 = (v3 - (q1.T @ v3) * q1 - (q2.T @ v3) * q2) / np.linalg.norm(v3 - (q1.T @ v3) * q1 - (q2.T @ v3) * q2)
print("v3:", v3)
print("q3:", q3)
print("length of q3:", np.linalg.norm(q3))
输出结果:
v3: [1. 0. 0. 1.]
q3: [ 0.69631062 -0.52223297 0.34815531 0.34815531]
length of q3: 0.9999999999999999
这样就得到列正交的$Q$矩阵
Q = np.array([q1, q2, q3]).T
Q # 4 x 3
输出结果:
array([[ 0.40824829, 0.12309149, 0.69631062],
[ 0.81649658, 0.24618298, -0.52223297],
[ 0. , 0.73854895, 0.34815531],
[ 0.40824829, -0.61545745, 0.34815531]])
对于上三角矩阵$R$,它的对角线元素为$v$扣除了在前面所有的$q$上的投影之后剩下的长度,而非对角线元素为$v$在前面的各个$q$上的投影量。
r11 = np.linalg.norm(v1)
r12 = q1.T @ v2
r22 = np.linalg.norm(v2 - (q1.T @ v2) * q1)
r13 = q1.T @ v3
r23 = q2.T @ v3
r33 = np.linalg.norm(v3 - (q1.T @ v3) * q1 - (q2.T @ v3) * q2)
R = np.array([
[r11, r12, r13],
[ 0, r22, r23],
[ 0, 0, r33]
])
R
输出结果:
array([[ 2.44948974, -0.40824829, 0.81649658],
[ 0. , 1.3540064 , -0.49236596],
[ 0. , 0. , 1.04446594]])
检验一下$QR$与$A$是否相等:
np.allclose(Q @ R, A)
输出结果:
True
再和numpy.linalg的结果比较一下:
np.linalg.qr(A)
输出结果:
(array([[-0.40824829, -0.12309149, -0.69631062],
[-0.81649658, -0.24618298, 0.52223297],
[-0. , -0.73854895, -0.34815531],
[-0.40824829, 0.61545745, -0.34815531]]),
array([[-2.44948974, 0.40824829, -0.81649658],
[ 0. , -1.3540064 , 0.49236596],
[ 0. , 0. , -1.04446594]]))
乍一看好像不一样但不要担心,只是$Q$和$R$都多了一个负号,相乘之后的结果仍然是一样的。
可以证明,对于列满秩的矩阵$A$,如果我们规定$R$的对角线元素为正,则QR分解式是唯一的。
热身结束,来看看代码怎么写。
Python代码
def CGS(A):
"""
Args:
A: (m x n) matrix with n linearly independent columns
Returns:
Q: (m x n) matrix with n orthonormal columns
R: (n x n) upper triangular matrix
"""
m, n = A.shape
Q = np.zeros(shape=(m, n))
R = np.zeros(shape=(n, n))
for j in range(n):
vj = A[:, j]
for i in range(j):
R[i, j] = Q[:, i].T @ A[:, j]
vj = vj - R[i, j] * Q[:, i]
R[j, j] = np.linalg.norm(vj)
Q[:, j] = vj / R[j, j]
return Q, R
CGS(A)
输出结果:
(array([[ 0.40824829, 0.12309149, 0.69631062],
[ 0.81649658, 0.24618298, -0.52223297],
[ 0. , 0.73854895, 0.34815531],
[ 0.40824829, -0.61545745, 0.34815531]]),
array([[ 2.44948974, -0.40824829, 0.81649658],
[ 0. , 1.3540064 , -0.49236596],
[ 0. , 0. , 1.04446594]]))
经典Gram-Schmidt算法还是比较直观的,给定向量$v$,不断扣除其在前面所有的$q$上的投影,扣完以后$v$就和它们正交了,只需再单位化即可,通过这种方式一个一个地造标准正交化向量。
而接下来所要谈的改良版Gram-Schmidt算法和它的区别是:给定向量$v$,改良版Gram-Schmidt先将$v$标准化得到$q$,然后将后面每一个还未正交化的向量都扣除其在$q$上的投影,这样一来,后面的每一个向量就都和$v$正交了。每一次迭代,后面的向量就会和当前的向量正交,而经典Gram-Schmidt算法是让当前的向量和之前所有的向量正交。
改良版Gram-Schmidt算法(MGS)
例子
第一步: 将$v_1$标准化得到$q_1$,然后将$v_2$和$v_3$都各自扣除它们在$q_1$上的投影
# v1
v1 = A[:, 0]
q1 = v1 / np.linalg.norm(v1)
# v2
v2 = A[:, 1]
v2 = v2 - (q1.T @ v2) * q1
# v3
v3 = A[:, 2]
v3 = v3 - (q1.T @ v3) * q1
print("q1:", q1)
print("length of q1:", np.linalg.norm(q1))
输出结果:
q1: [0.40824829 0.81649658 0. 0.40824829]
length of q1: 1.0
第二步: 将$v_2$标准化得到$q_2$,然后将$v_3$扣除它在$q_2$上的投影
# v2
q2 = v2 / np.linalg.norm(v2)
# v3
v3 = v3 - (q2.T @ v3) * q2
print("q2:", q2)
print("length of q2:", np.linalg.norm(q2))
输出结果:
q2: [ 0.12309149 0.24618298 0.73854895 -0.61545745]
length of q2: 0.9999999999999999
第三步: 将$v_3$标准化得到$q_3$
# v3
q3 = v3 / np.linalg.norm(v3)
print("q3:", q3)
print("length of q3:", np.linalg.norm(q3))
输出结果:
q3: [ 0.69631062 -0.52223297 0.34815531 0.34815531]
length of q3: 1.0
输出结果:
Q = np.array([q1, q2, q3]).T
Q
输出结果:
array([[ 0.40824829, 0.12309149, 0.69631062],
[ 0.81649658, 0.24618298, -0.52223297],
[ 0. , 0.73854895, 0.34815531],
[ 0.40824829, -0.61545745, 0.34815531]])
结果和CGS算法一致。
上三角矩阵$R$的主对角线元素仍然为$v$扣除了在前面所有的$q$上的投影后剩下的长度,而非主对角线元素的计算顺序发生了变化:对每一行按照自左向右的顺序计算$v$后面的每一个向量在$q$上的投影量(CGS是对每一列按自上而下的顺序进行计算)。
v1 = A[:, 0]
v2 = A[:, 1]
v3 = A[:, 2]
# 当前向量为v1,后面的向量为v2, v3
r11 = np.linalg.norm(v1)
r12 = q1.T @ v2
r13 = q1.T @ v3
v2 = v2 - r12 * q1
v3 = v3 - r13 * q1
# 当前向量为v2,后面的向量为v3
r22 = np.linalg.norm(v2)
r23 = q2.T @ v3
v3 = v3 - r23 * q2
# 当前向量为v3
r33 = np.linalg.norm(v3)
# 结果
R = np.array([
[r11, r12, r13],
[ 0, r22, r23],
[ 0, 0, r33]
])
R
输出结果:
array([[ 2.44948974, -0.40824829, 0.81649658],
[ 0. , 1.3540064 , -0.49236596],
[ 0. , 0. , 1.04446594]])
Python代码
def MGS(A):
"""
Args:
A: (m x n) matrix with n linearly independent columns
Returns:
Q: (m x n) matrix with n orthonormal columns
R: (n x n) upper triangular matrix
"""
m, n = A.shape
V = A.copy().astype('float64') # A's dtype maybe int64, which must be converted to float to avoid implicit conversion of float to integer
Q = np.zeros(shape=(m, n))
R = np.zeros(shape=(n, n))
for i in range(n):
R[i, i] = np.linalg.norm(V[:, i])
Q[:, i] = V[:, i] / R[i, i]
for j in range(i + 1, n):
R[i, j] = Q[:, i].T @ V[:, j]
V[:, j] = V[:, j] - R[i, j] * Q[:, i] # implicit conversion may occur here if we do not convert dtype to float at first
return Q, R
MGS(A)
输出结果:
(array([[ 0.40824829, 0.12309149, 0.69631062],
[ 0.81649658, 0.24618298, -0.52223297],
[ 0. , 0.73854895, 0.34815531],
[ 0.40824829, -0.61545745, 0.34815531]]),
array([[ 2.44948974, -0.40824829, 0.81649658],
[ 0. , 1.3540064 , -0.49236596],
[ 0. , 0. , 1.04446594]]))
改良版Gram-Schmidt算法的优点在于其数值稳定性,这又是另外一块内容了。
通过Householder变换的方法
Gram-Schmidt:三角正交化
通过上面的例子可以看到,不管是经典的Gram-Schmidt算法还是改良版的,它们都是在矩阵$A$的右边不断地乘以上三角矩阵。
令
于是,
则
这里$R^{-1}=R_1^{-1} R_2^{-1} R_3^{-1}$和$R’^{-1}=R_1’^{-1}R_2’^{-1}R_3’^{-1}$也是上三角矩阵(上三角矩阵的逆以及乘积仍然为上三角)。
Gram-Schmidt算法是不断地地乘上三角矩阵,所以又被称为三角正交化,而接下来要介绍的Householder变换法则被称为正交三角化。
Householder: 正交三角化
QR分解中$Q$和$R$的地位应该是同等的,既然我们可以通过在$A$的右边不断乘上三角矩阵得到$Q$,那么另一种自然的想法就是:能不能在$A$的左边不断地乘正交矩阵最后得到$R$?
答案是肯定的。Householder巧妙地设计了一系列正交矩阵$Q_k$,使得$Q_n \cdots Q_2 Q_1 A$为上三角矩阵,其基本思路如下:
- $Q_1$把$A$的第一列第一行以下的所有元素都映乘0;
- $Q_2$保持$A$的第一列不变,将第二列第二行以下的所有元素都映乘0;
- $Q_3$保持$A$的前两列不变,将第三列第三行以下的所有元素都映乘0;
- 依此类推,$Q_k$保持$A$的前$k-1$列不变,将第$k$列第$k$行以下的所有元素都映乘0。例如:
那么该如何设计正交矩阵$Q_k$呢?
Householder镜射矩阵
假设我们已经迭代了$k-1$次,则矩阵$A$变为$Q_{k-1} \cdots Q_2 Q_1 A$,再作用正交矩阵$Q_k$后,我们希望保持前$k-1$列不变,并且第$k$列第$k$个元素以下的所有元素都映成0。可以考虑将$m\times m$阶正交矩阵$Q_k$进行分块:
这里$I$是$k-1$阶单位矩阵,负责保持前$k-1$列不变,$F$是一个$(m-k+1)\times(m-k+1)$正交矩阵,其作用是从$A$的第$k$列的最后$m-k+1$行中“提取并加工”第一个元素而将其它元素都映为0。例如,当$m=4$,$k=3$时,$F$为一个$2\times2$正交矩阵,它可以提取一个2维向量的第一个元素而将第二个元素映成0,这个正交矩阵$F$就是Householder镜射矩阵。
令$x\in \mathbb{R}^{m-k+1}$为$F$所要提取的向量(即$A$的第$k$列的最后$m-k+1$行所组成的向量),则$F$的作用结果为:
可以看到经过$F$作用以后$x$的长度保持不变,只不过全都集中到了第一个分量里,因此$F$就像是$\mathbb{R}^{m-k+1}$空间里的一面镜子(事实上是一个超平面),它把其它向量都映射到第一个坐标轴上,如下图所示:
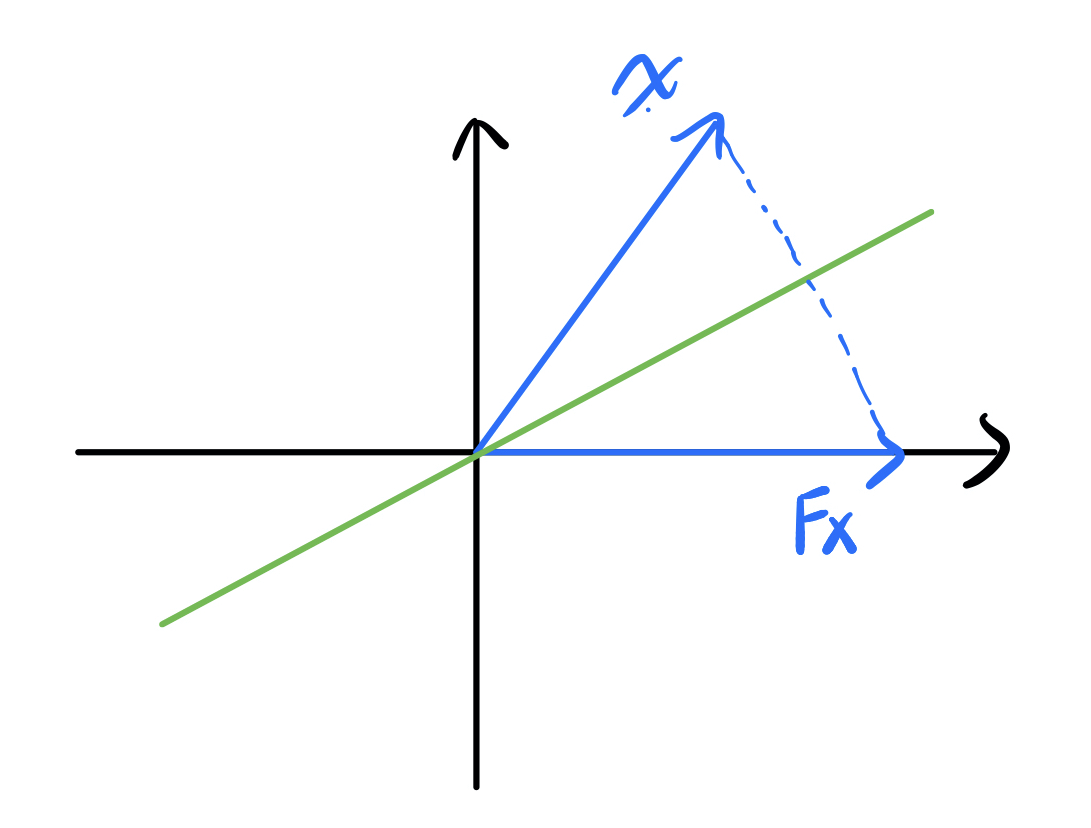
以上只是把$x$映到正的情况,当然还存在另一面镜子把$x$映到负的:
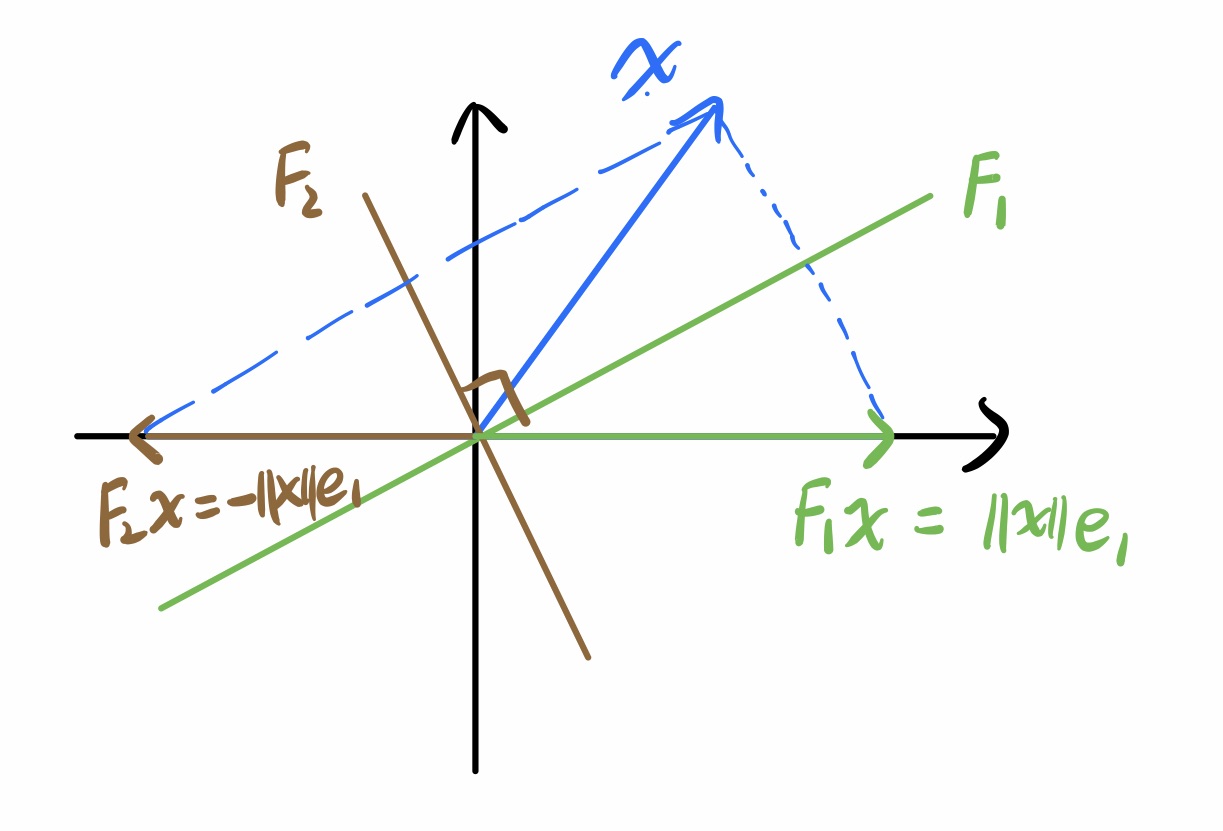
到底用哪一面镜子涉及到数值稳定性,我们稍后再讲,先来看看怎么得到其中一面镜子。
以$F_1$为例,令$v=\left\lVert x\right\rVert e_1 - x$为与镜子垂直的方向向量,$w$为$-x$在$v$上的投影$\frac{-v^Tx}{v^Tv}v$,则
因此,镜射矩阵为
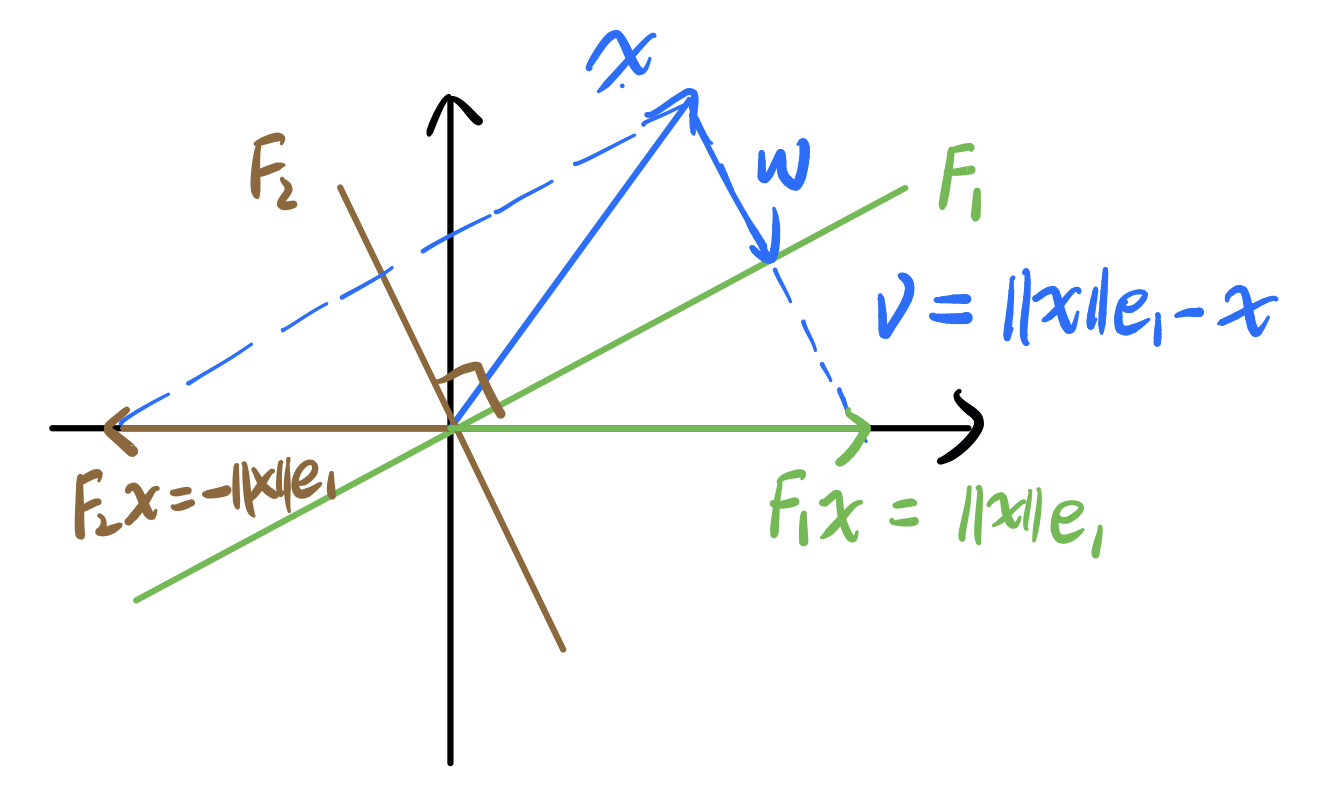
注意到$F = I - 2 \frac{v v^T}{v^T v}$是满秩矩阵,因为只有0向量才会被映到0,即$F$的零空间只有0向量,所以它是满秩的。
接下来从数值稳定性的角度考虑要选哪一面镜子。我们知道,$x$ 经过 $F$ 映射后的结果为 $\pm\left\lVert x\right\rVert e_1$,而为了计算$F$必须先求出改变量 $v=\pm\left\lVert x\right\rVert e_1 - x$,如果$v$很小的话,由于计算机舍入误差(rouding error)的存在就会导致$F$的计算结果不稳定。因此,我们更偏向于较大的$v$所对应的那面镜子。从上面的图可以看到,当 $x$ 的第一个分量 $x_1$ 为正时,选 $F_2$ 当镜子的改变量 $v$ 更大,不难想象,当 $x_1$ 为负时,选 $F_1$ 当镜子的改变量更大,也就是说,我们的选择和 $x_1$ 的符号正好相反。因此, $v=-\text{sign}(x_1)\left\lVert x\right\rVert e_1 - x$,或者我们可以提出-1(因为 $vv^T$ 负负得正对 $F$ 没有影响),得到
算法
假设给定矩阵 $m$ x $n$ 矩阵 $A$,$m \ge n$。令 $Q^{(0)}$ 为 $m$ 阶单位矩阵,$A^{(0)}$ 为 $A$,将它们都乘以 $n$ 个正交矩阵 $Q_k$ 得
这里
其中,$F_{m-k+1}$ 为前面所讲的Householder镜射矩阵。
Python代码
def householder_qr(A):
"""
Args:
A: (m x n) matrix
Returns:
Q: (m x m) orthogonal matrix
R: (m x n) upper triangular matrix with zeros below
"""
m, n = A.shape
Q = np.eye(m)
for k in range(n):
Q_k = np.eye(m)
Q_k[k:, k:] = make_householder(A[k:, k]) # replace with Householder matrix
A = Q_k @ A # A updates to R
Q = Q @ Q_k # Identity updates to Q
return Q, A
def make_householder(x):
"""
Constructs the Householder matrix, given the column which we want to mirror to the e1 axis.
Args:
x: the column vector we want to mirror
Returns:
F: the Householder matrix
"""
e1 = np.zeros(x.size)
e1[0] = 1.0
v = sign(x[0]) * np.linalg.norm(x) * e1 + x
v = v / np.linalg.norm(v)
v = v.reshape((x.size, -1)) # make v a column vector instead of a numpy array so that the '@' operator applies
F = np.eye(x.size) - 2 * v @ v.T
return F
def sign(x):
"""
Returns 1 if x >= 0, -1 otherwise.
"""
sign = 1
if x < 0:
sign = -1
return sign
Q, R = householder_qr(A)
Q
输出结果:
array([[-4.08248290e-01, -1.23091491e-01, -6.96310624e-01,
-5.77350269e-01],
[-8.16496581e-01, -2.46182982e-01, 5.22232968e-01,
-5.55111512e-17],
[ 0.00000000e+00, -7.38548946e-01, -3.48155312e-01,
5.77350269e-01],
[-4.08248290e-01, 6.15457455e-01, -3.48155312e-01,
5.77350269e-01]])
R
输出结果:
array([[-2.44948974e+00, 4.08248290e-01, -8.16496581e-01],
[ 2.20794948e-17, -1.35400640e+00, 4.92365964e-01],
[-3.00282564e-16, -1.03279116e-16, -1.04446594e+00],
[-1.52833015e-16, 4.07354380e-17, 0.00000000e+00]])
得到和前两种算法相同的结果。